Collider Smart Contract

Author: sshmatrix | github | quant/acc | q/acc

Ping: [email protected]

This is a living document and will be updated in real time to match the development of the actual product.

Overview

This program implements a decentralised prediction market using two competing tokens - $ANTI and $PRO . The architecture flows from a single program ID down to individual token accounts:

• Program initialises with a state account tracking all created polls
• Each poll is derived as a PDA from the poll counter
• Polls manage paired $ANTI - $PRO token accounts for market positions
• Users deposit tokens to take market positions
• After poll end, smart contracts handle token settlement

Figure 1: Overview

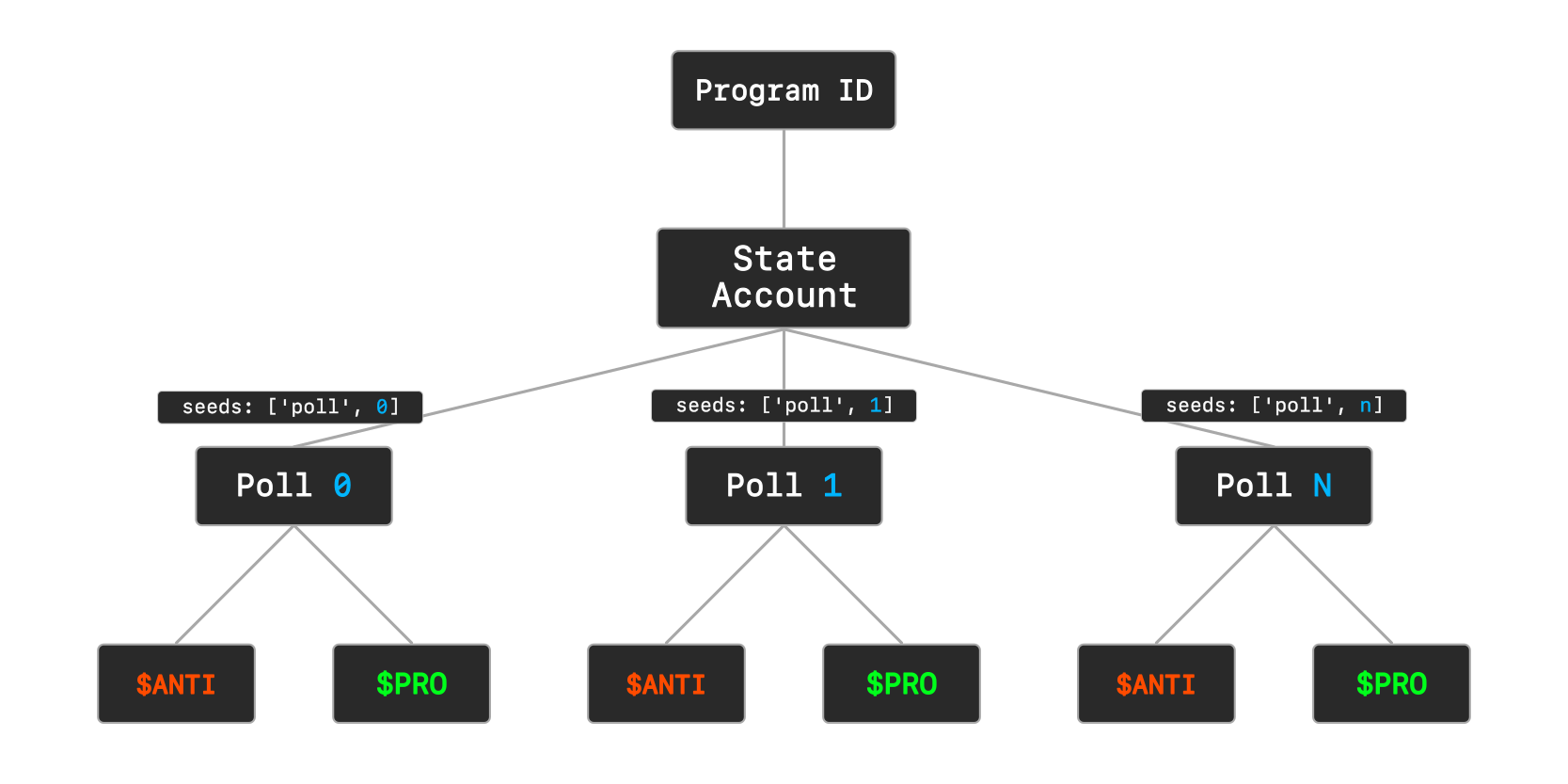
Structure

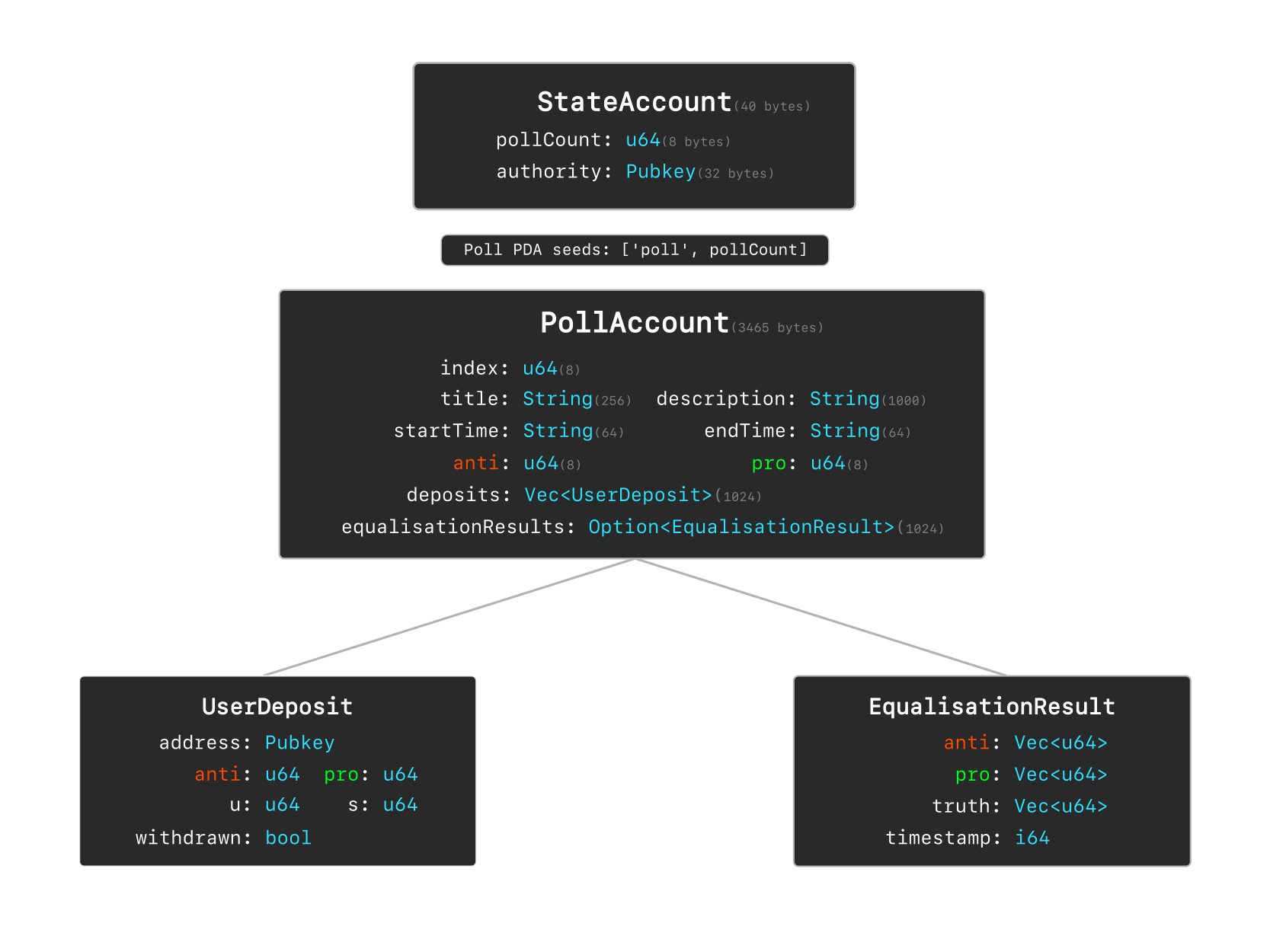
State Account

• Central authority account managing poll creation
• Tracks total polls and program authority
• Fixed size: 8 bytes for poll counter + 32 bytes for authority pubkey

Poll Account

• Created per prediction market poll
• Derived using PDA seeds: ['poll', poll_index]
• Contains poll metadata, deposits, and results:
  • String fields:
    • title (256 bytes)
    • description (1000)
    • start_time (64 bytes)
    • end_time (64 bytes)
  • Token tracking:
    • Total $ANTI in each prediction pool (16 bytes)
    • Total $PRO in each prediction pool (16 bytes)
  • deposits vector (1024 bytes)
  • Optional equalisation_results (1024 bytes)

Data Structures

UserDeposit

• Tracks individual user deposits
• Records $ANTI - $PRO amounts, truth values
• Includes withdrawn status

EqualisationResult

• Stores final poll outcomes
• $ANTI - $PRO token return amounts
• Truth value distributions
• Settlement timestamp

The red/green color scheme differentiates between $ANTI / $PRO token flows through the system accounts.

Figure 2: Core

Events

The program emits events at key state transitions for off-chain indexing:

PollCreatedEvent

{
    poll_index: u64,     // Unique identifier
    address: Pubkey,     // Poll creator
    title: String,       // Poll title
    description: String, // Poll description
    start_time: String,  // ISO timestamp
    end_time: String,    // ISO timestamp
    timestamp: i64       // Creation time
}

DepositEvent

{
    poll_index: u64,      // Referenced poll
    address: Pubkey,      // Depositor address
    anti: u64,            // $ANTI deposit amount
    pro: u64,             // $PRO deposit amount
    u: u64,               // Truth value u
    s: u64,               // Truth value s
    timestamp: i64        // Deposit time
}

EqualisationEvent

{
    poll_index: u64,      // Referenced poll
    truth: Vec<u64>,      // Final truth values
    anti: u64,            // Total $ANTI pooled
    pro: u64,             // Total $PRO pooled
    timestamp: i64        // Equalisation time
}

WithdrawEvent

{
    poll_index: u64,      // Referenced poll
    address: Pubkey,      // Withdrawer address
    anti: u64,            // $ANTI withdrawn
    pro: u64,             // $PRO withdrawn
    timestamp: i64        // Withdrawal time
}

These events enable off-chain indexing for market analytics, user positions tracking, and historical data analysis.

Functions

equalise()

This function redistributes tokens after truth is fed to the program by the authority. It relies on internal function overlap() .

Rust Code

pub fn equalise(
    deposits: &[UserDeposit],
    anti: u64,
    pro: u64,
    truth: &[u64],
) -> Result<(Vec<u64>, Vec<u64>)> {
    const NUM_BINS: usize = 100;
    let bin_size = BASIS_POINTS / NUM_BINS as u64;

    // Initialise bins
    let mut bins = vec![0u64; NUM_BINS];
    let mut items_in_bins = vec![Vec::new(); NUM_BINS];
    let mut value_sums = vec![(0u64, 0u64); NUM_BINS];

    // Calculate normalised overlap with truth
    let mut overlap_values = Vec::with_capacity(deposits.len());
    for deposit in deposits {
        let parity = if (truth[0] > truth[1]) == (deposit.anti > deposit.pro) {
            1i64
        } else {
            -1i64
        };

        let baryon = deposit.u;
        let photon = deposit.s;

        // Calculate overlap value
        let overlap = overlap(baryon, photon, parity)?;
        overlap_values.push(overlap);
    }

    // Populate bins
    for (i, &overlap) in overlap_values.iter().enumerate() {
        if overlap <= BASIS_POINTS {
            let bin_index = (overlap / bin_size) as usize;
            let bin_index = bin_index.min(NUM_BINS - 1);

            bins[bin_index] += 1;
            items_in_bins[bin_index].push(i);
            value_sums[bin_index].0 += deposits[i].anti;
            value_sums[bin_index].1 += deposits[i].pro;
        }
    }

    // Calculate distribution and returns
    let mut anti = vec![0u64; deposits.len()];
    let mut pro = vec![0u64; deposits.len()];

    for (bin_idx, indices) in items_in_bins.iter().enumerate() {
        if indices.is_empty() {
            continue;
        }

        let bin_anti_total = value_sums[bin_idx].0;
        let bin_pro_total = value_sums[bin_idx].1;

        for &deposit_idx in indices {
            let deposit = &deposits[deposit_idx];

            // Calculate proportional returns
            if bin_anti_total > 0 {
                anti[deposit_idx] = (deposit.anti * anti) / bin_anti_total;
            }
            if bin_pro_total > 0 {
                pro[deposit_idx] = (deposit.pro * pro) / bin_pro_total;
            }
        }
    }

    Ok((anti, pro))
}

Rust Utils

a. overlap()

// Overlap calculator
fn overlap(baryon: u64, photon: u64, parity: i64) -> Result<u64> {
    const TWO_E9: u64 = 2_000_000_000;

    if baryon >= TWO_E9 {
        return Ok(0);
    }

    let x = TWO_E9 - baryon;
    let log_x = (BASIS_POINTS * x.ilog2() as u64) / 10; // Simplified log calculation

    let photon_term = if photon <= BASIS_POINTS {
        BASIS_POINTS
    } else {
        BASIS_POINTS + (BASIS_POINTS * photon.ilog2() as u64) / 10
    };

    let result = if parity > 0 {
        (BASIS_POINTS * BASIS_POINTS) / (BASIS_POINTS + log_x / photon_term)
    } else {
        (log_x * photon_term) / BASIS_POINTS
    };

    Ok(result.min(BASIS_POINTS))
}

Javascript Code

The equivalent code in Javascript is:

/* Calculates gains using truth (= [μ, σ]) */
export const equalise = (
  baryonBalances,
  photonBalances,
  antiBalances,
  proBalances,
  antiPool,
  proPool,
  prices,
  wallets,
  truth
) => {
  // Calculate normalised overlap with truth (inverse-log-normalised)
  const overlap = baryonBalances
    .map((_, i) => {
      const baryon = baryonBalances[i];
      const photon = photonBalances[i];
      const parity =
        truth.length === 0
          ? 0
          : truth[0] > truth[1] === antiBalances[i] > proBalances[i]
          ? 1
          : -1;

      return (
        parity *
        Math.exp(
          -Math.pow(Math.log(2e9 - baryon), 2) /
            (2 * Math.pow(photon <= 1 ? 1 : 1 + Math.log(photon), 2))
        )
      );
    })
    .map((value) => {
      if (value === 0) return 0;
      if (value === 1) return 1;
      if (value > 0) return 1 / Math.abs(Math.log(value));
      return 1 - 1 / Math.abs(Math.log(Math.abs(value)));
    });

  // Calculate forward distribution
  const forward = distributer(overlap, [], [], antiBalances, proBalances);

  // Calculate returns
  const scatter = {
    anti: scatterer(forward.distribution, antiPool),
    pro: scatterer(forward.distribution, proPool),
    baryon: [],
    photon: [],
  };

  const returns = [
    localiser(scatter.anti.resampled, forward.indices, antiBalances),
    localiser(scatter.pro.resampled, forward.indices, proBalances),
    [],
    [],
  ];

  // Calculate inversions
  const equalised = {
    anti: Array(wallets.length).fill(0),
    pro: Array(wallets.length).fill(0),
    baryon: Array(wallets.length).fill(0),
    photon: Array(wallets.length).fill(0),
    wallet: Array(wallets.length).fill(0),
    indices: Array(wallets.length).fill(0),
  };
  let _counter_ = 0;
  for (let i = 0; i < returns[0].length; i++) {
    for (let j = 0; j < returns[0][i].length; j++) {
      const _anti = returns[0][i][j];
      const _pro = returns[1][i][j];
      equalised.anti[forward.indices[i][j]] = _anti;
      equalised.pro[forward.indices[i][j]] = _pro;
      const collide = collide(_anti, _pro);
      const _baryon = collide.u;
      const _photon = collide.s;
      equalised.baryon[forward.indices[i][j]] = _baryon;
      equalised.photon[forward.indices[i][j]] = _photon;
      equalised.wallet[forward.indices[i][j]] = wallets[_counter_];
      _counter_ += 1;
      equalised.indices.push(forward.indices[i][j]);
    }
  }

  // Calculate changes
  const change = {
    baryon: [],
    photon: [],
    anti: antiBalances.map((value, index) => equalised.anti[index] - value),
    pro: proBalances.map((value, index) => equalised.pro[index] - value),
    gain: antiBalances.map(
      (value, index) =>
        (equalised.anti[index] - value) * prices[0] +
        (equalised.pro[index] - proBalances[index]) * prices[1]
    ),
    original: antiBalances.map(
      (value, index) => value * prices[0] + proBalances[index] * prices[1]
    ),
    wallets: wallets,
  };

  return {
    overlap: overlap,
    normalised: Math.max(...overlap)
      ? overlap.map((x) => 1 - x / Math.max(...overlap))
      : overlap.map((x) => 1 - x),
    equalised,
    change,
  };
};

JS Utils

The equalise() function depends on four helper functions: distributer() , scatterer() , localiser() and collide() , with additional invert() for explicit handle on $BARYON and $PHOTON .

a. distributer()

// Distribute indexed values over bins
function distributer(
  values,
  baryonBalances,
  photonBalances,
  antiBalances,
  proBalances,
  numBins = 100
) {
  // Step 1: Initialise bins
  const bins = Array(numBins).fill(0);
  const binSize = 1 / numBins;
  const itemsInBins = Array(numBins)
    .fill(null)
    .map(() => []);
  const valueInBins = Array(numBins)
    .fill(null)
    .map(() => []);

  // Step 2: Populate bins based on the values
  values.forEach((value, index) => {
    if (value >= 0 && value <= 1) {
      const binIndex = Math.min(Math.floor(value / binSize), numBins - 1);
      bins[binIndex] += 1; // Increment the corresponding bin
      itemsInBins[binIndex].push(index);
      valueInBins[binIndex].push([
        baryonBalances[index],
        photonBalances[index],
        antiBalances[index],
        proBalances[index],
      ]);
    }
  });

  // Step 3: Normalise the distribution
  const totalValues = values.length;
  const distribution = bins.map((count) => count / totalValues);

  // Calculate piecewise sums of all tokens in each bin separately
  const valueSums = valueInBins.map((binArray) => {
    return binArray.reduce(
      (binTotals, fourArray) => {
        return [
          binTotals[0] + fourArray[0],
          binTotals[1] + fourArray[1],
          binTotals[2] + fourArray[2],
          binTotals[3] + fourArray[3],
        ];
      },
      [0, 0, 0, 0]
    );
  });

  return {
    distribution: bins,
    normalised: distribution,
    indices: itemsInBins,
    values: valueSums,
  };
}

b. scatterer()

// Distributes values across bins based on another distribution
function scatterer(distribution, totalCount) {
  // Find indices of non-zero bins
  const nonZeroBinIndices = distribution
    .map((value, index) => ({
      value,
      index,
    }))
    .filter((item) => item.value > 0)
    .map((item) => item.index);

  // Initialise result array with zeros
  const resampled = new Array(distribution.length).fill(0);
  // Calculate values for non-zero bins before normalisation
  const totalBinValues = nonZeroBinIndices.length + 1;
  const unnormalised = nonZeroBinIndices.map(
    (index) => (index + 1) / totalBinValues
  );

  // Calculate sum of unnormalised values distribution
  const totalUnnormalised = unnormalised.reduce((sum, val) => sum + val, 0);

  // Normalise and assign only to non-zero bin positions
  nonZeroBinIndices.forEach((binIndex, i) => {
    resampled[binIndex] =
      (unnormalised[nonZeroBinIndices.length - 1 - i] / totalUnnormalised) *
      totalCount;
  });

  return {
    resampled,
  };
}

c. localiser()

// Distributes values within one bin
function localiser(valueSums, indicesInBins, orderBy) {
  return valueSums.map((sums, binIndex) => {
    const count = indicesInBins[binIndex].length;
    if (count === 0) return [];
    if (count > 1) {
      const binIndices = indicesInBins[binIndex];
      const orderValues = binIndices.map((i) => orderBy[i]);
      const total = orderValues.reduce((a, b) => a + b, 0);
      if (total > 0) {
        return orderValues.map((v) => (v / total) * sums);
      } else {
        return Array(count).fill(sums / count);
      }
    }
    return Array(count).fill(sums / count);
  });
}

d. collide()

// Calculates mean and standard deviation of prediction
const collide = (anti, pro) => {
  // Step 1: Calculate u (= mean)
  const u = anti + pro >= 0 && anti + pro < 1 ? 0 : Math.abs(anti - pro);

  // Step 2: Calculate s (= standard deviation)
  const s =
    (anti + pro >= 0 && anti + pro < 1) || Math.abs(anti - pro) <= anti + pro
      ? 0
      : Math.abs(anti - pro) < 1
      ? anti + pro
      : (anti + pro) / Math.abs(anti - pro);

  return {
    u,
    s,
  };
};

e. invert()

// Inverts equalised emissions to tokens
export const invert = (baryon, photon, parity) => {
  // Step 1: Calculate anti
  const anti =
    baryon > 0
      ? photon > 0 && baryon >= 1 && photon >= 1
        ? 0.5 * baryon * (photon + parity)
        : baryon >= 1
        ? 0
        : 0.5 * baryon
      : 0.5 * photon;

  // Step 2: Calculate pro
  const pro =
    baryon > 0
      ? photon > 0 && baryon >= 1 && photon >= 1
        ? 0.5 * baryon * (photon - parity)
        : baryon >= 1
        ? 0
        : 0.5 * baryon
      : 0.5 * photon;

  return {
    anti,
    pro,
  };
};